Engineered Patterns in Biology III: Cheetah Spots in Bacteria

The first article in this series was an introduction to Turing pattern formation, it briefly covered the theory behind the formula, where it is generally applied and experimental proof confirming the theory. In the second article, I explained briefly the concept of genetic circuits; comparing genetics to electronic circuits, and a brief explanation of the mechanism of a simple genetic toggle switch circuit. Here, I am going to bring these two branches of science together to try to explain how to construct a genetic circuit that produces patterns in Turing instability fashion. This is a theoretical exercise, we assume that the biological parts chosen here behave exactly as we want them to behave, which is not necessarily true all the time. I will not cover biological details behind the choice of promoters and genes, instead, we will have an engineering mentality of picking components from the shelf approach. As we will see later, it works in the real world

Design From First Principles

Recall from the first article that the hypothesis Turing made is the existence of at least two molecules – or morphogens– that diffuse between cells and react with each other to produce patterns. Thus, we have to choose genes that can be synthesised within the cell but diffuse to other cells and react in such a way to regulate the gene synthesis of other cells. It is helpful to break the problem into two parts; first, a cell to cell communications design, then cell regulations mechanism –given the communication signals– as illustrated below in figure 1:

Fig1: The top figure is showing a simplified cartoon of a two-way communication system between cells using morphogens. The bottom figure the possibility of having a regulation mechanism as a function of the morphogens

Cell-Cell Communication

We require two conditions for cell-cell communication; First, the communication molecules –or morphogens– have to be synthesised within the cells and diffused to other cells. Second, given two morphogens A and B, morphogen A activates the synthesis of morphogen B, while morphogen B inhibits the synthesis of morphogen A, as illustrated below (figure 2). The second criterion will be covered in depth later.

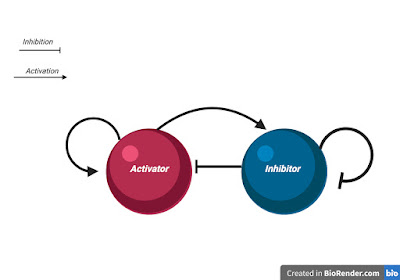Fig2: Morphogen dynamics according to Turing criterion to achieve Turing instabilities

As for the first condition, luckily there exists such a mechanism in nature already called quorum sensing. All we have to do is borrow it from the many strains of bacteria that use quorum sensing to communicate with each other [1]; namely, we borrow the Las and Rhl quorum-sensing pathways from Pseudomonas aeruginosa bacteria, using one of the pathways for activation while the other for inhibition. Both pathways consist of two genes, the las system consist of LasI and LasR genes (The names aren't necessary but their dynamics are) [2], LasI gene synthesis A3OC12HSL proteins, let's call it "A" proteins from now. These proteins diffuse between cells which make them great for talking to other cells. Remember that the whole point of communicating with other cells is to regulate the synthesis of genes, this is where the second part of the las system is useful. LasR genes synthesis proteins to combine with "A" proteins to form an activation transcription factor that can be used to regulate any gene given the appropriate choice of upstream promoters which is illustrated with a simple sketch below.

Fig3: simple sketch illustrating the dynamics between activators and RNA polymerase [3]

We will cover the promoter choices to be regulated by the A-LasR complex transcription factor later, we must now cover the Rhl mechanism. Similar to the Las system, it consists of two genes, RhII gene is responsible for signalling between cells by producing IC4HSL proteins (abbreviated as "I"). The other gene –named RhIR– helps with the regulation by forming a transcription factor complex with the IC4HSL protein. We must now satisfy Turing's instability approach by choosing one signalling molecule to behave as an activator and the other to behave as an inhibitor. As these molecules only activate the promoters, allowing for the synthesis of the promoter's downstream genes; one must add one more gene to block the synthesis; we use cl gene for this task, this gene function naturally in bacteriophage, which will be explained thoroughly below.

Molecule-Cell Regulation

At this time, it is helpful to go back to the reaction-diffusion model in order to establish the regulation dynamics:

The degradation rates are usually determined empirically due to the nature of proteins to degrade.  We have already established that our molecules diffuse in the spatial domain to other cells, one thing remains is to define the reaction term functions f(A,I) and g(A,I). Recall the rules of Turing morphogens represented in figure 2 indicate a positive feedback mechanism with the activator (the more activators there are, the more we are making of them). On the other hand, negative feedback exists with the inhibitor by inhibiting the production of itself. The activator initialises the synthesis of itself while the inhibitor blocks the synthesis of the activator, a pretty unhealthy relationship from a social perspective. Using the node interaction sketch in figure 2, we can expand the reaction functions to be:

We are assuming above that the activation of both morphogens is a function of the activator solely (v(A) and r(A))  and the inhibition is a function of the inhibitor only for both morphogens (u(I) and r(I)). Betas and lambdas are merely proportion parameters. Recall that transcription factors form by combining two proteins, A with LasR and I with RhIR, thus we could refine our activation functions:

One could initially approximate the activation transcription factor as a simple product between A and LasR, in other words, the concentration of the activation transcription factor is approximately:

We have enough information now to draw a simple diagram illustrating the dynamics of the activation regulatory network as shown below.

As for the inhibition regulatory network, we have to include one more gene (C) to act as an inhibitor, because the I- IC4HSL only activates promoters to initiate transcription downstream rather than inhibiting them as mentioned earlier, so I- IC4HSL will activate C  gene that will inhibit promoters directly. We can still use the approximation of the concentration of the transcription factor to be equal to the product of the two molecules and assume it to equal to the concentration of C, so:

where epsilon in the equation above refers to the proportionality constant. Again, we can depict the dynamics graphically:

Assembly and Results

We have now covered a qualitative view of genetically modifying E. coli to produce patterns using first principles from the reaction-diffusion model. Further biological details such as the exact choices of promoters can be found on the amazing paper by Ron Weiss et. al [4]. Their work also refines the models even further by using stochasticity in the reaction-diffusion model to match the results in the real world. Below in figure 4 is the results obtained by implementing the reaction-diffusion inspired circuit to express green fluorescent proteins (GFP) on the right and red fluorescent protein on the left, the spot-like pattern can be easily seen the population of E. coli. 

Fig 5: Experiment results showing the circuit working and giving spot like pattern in a population of E.coli

[1] BL, M., 2001. Quorum Sensing In Bacteria. - Pubmed - NCBI. [online] Ncbi.nlm.nih.gov. Available at: <https://www.ncbi.nlm.nih.gov/pubmed/11544353> [Accessed 5 May 2020].

[2] Pearson, J., Pesci, E. and Iglewski, B., 1997. Roles of Pseudomonas aeruginosa las and rhl quorum-sensing systems in control of elastase and rhamnolipid biosynthesis genes. Journal of bacteriology, 179(18), pp.5756-5767.

[3] Khan Academy, 2020. Transcription Factors (Article) | Khan Academy. [online] Khan Academy. Available at: <https://www.khanacademy.org/science/biology/gene-regulation/gene-regulation-in-eukaryotes/a/eukaryotic-transcription-factors> [Accessed 20 May 2020].

[4] Karig, D., Martini, K., Lu, T., DeLateur, N., Goldenfeld, N. and Weiss, R., 2018. Stochastic Turing patterns in a synthetic bacterial population. Proceedings of the National Academy of Sciences, 115(26), pp.6572-6577.